4.1: Reference Angles

• Roy Simpson
• Cosumnes River College

Learning Objectives

• Identify the reference angle for an angle given in standard position.
• Evaluate a trigonometric function at a non-acute angle using the reference angle.
• Use technology to approximate the value of a trigonometric function at a non-acute angle.
• Determine an angle given the quadrant in which the angle terminates and the value of a trigonometric function.

The town of Avery lies 48 miles due east of Baker, and Clio is 34 miles in the bearing \( \mathrm \, 35^ < \circ >\, \mathrm \) from Baker. How far is it from Avery to Clio?

We know how to solve right triangles using the trigonometric ratios; however, the triangle formed by the three towns is not a right triangle because it includes an obtuse angle of \(125^\) at \(B\), as shown in Figure \( \PageIndex < 1 >\).

This type of triangle is called an oblique triangle. Later in this course, we learn how to solve oblique triangles, but first, we must be able to find the values of the trigonometric functions for obtuse angles.

Reference Angles

We now introduce an essential tool for evaluating trigonometric functions and solving trigonometric equations involving non-acute angles.

Definition: Reference Angle

The reference angle for an angle \( \theta \) in standard form is the acute angle formed between the terminal side of \( \theta \) and the \( x \)-axis. By convention, the reference angle is always considered positive (even if it opens in a clockwise direction). It is denoted with the "hat" notation, \( \hat \).

Any acute angle \(\theta\) is the reference angle for four angles between \(0^\) and \(360^\), one in each quadrant. The figure below shows the four angles in standard position whose reference angle is \(35^\). Note that each angle is found by measuring \(35^\) from the \(x\)-axis in the appropriate quadrant and that the four angles together make a "bow-tie" shape.

Example \(\PageIndex\)

Find and label the reference angle for the given angle.

1. \( A = 125^ < \circ >\)
2. \( B = 240^ < \circ >\)
3. \( \alpha = 310^ < \circ >\)
4. \( \beta = -315^ < \circ >\)
5. \( t = 820^ < \circ >\)

1. We begin by sketching the angle and its terminal side. Since the terminal side of \( A \) is in \( \mathrm \), the smallest angle that gets us directly to the \( x \)-axis can be found by imagining we rotated to the negative \( x \)-axis (\( 180^ < \circ >\)) and then backed off by \( \hat \) to get to \( A = 125^ < \circ >\). Mathematically, this is \( 180^ < \circ >- 125^ < \circ >= 55^ < \circ >\). Hence, the reference angle for \( A \) is \( \hat = 55^ < \circ >\).
2. Again, sketch the original angle and its terminal side. \( B \in \mathrm \), so the smallest angle to the \( x \)-axis can be found by imagining we rotated to the negative \( x \)-axis (\( 180^ < \circ >\)) and then added the reference angle \( \hat \) to get to \( B = 240^ < \circ >\). That is, \( 180^ < \circ >+ \hat = 240^< \circ >\). Therefore, \( \hat = 240^ < \circ >- 180^ < \circ >= 60^ < \circ >\) (see the figures below).
3. A quick sketch shows that \( \alpha \in \mathrm \). To find the reference angle, we imagine rotating in a full circle (\(360^< \circ >\)) and backing off by the angle \( \hat \) to arrive at \( 310^ < \circ >\). Therefore, \( 360^ < \circ >- \hat = 310^< \circ >\). Hence, \( 360^ < \circ >- 310^ < \circ >= 50^ < \circ >= \hat \) (see the figures below).
4. \( \beta \) being a negative angle doesn't change the tactic too much. We sketch \( \beta = -315^ < \circ >\) and its terminal side. Since \( \beta \) terminates in \( \mathrm \), we can imagine finding the reference angle by rotating a full revolution in the negative direction (\( -360^ < \circ >\)) and backing off by \( \hat \) to arrive at \( \beta = -315^ < \circ >\). "Backing off" in this instance means "adding back" \( \hat \). Therefore, we want to compute \( -360^ < \circ >+ \hat = -315^< \circ >\). Solving this equation yields \( \hat = 45^ < \circ >\) (see the figures below).
5. When an angle is outside of the interval \( \left( -360^< \circ >, 360^ < \circ >\right) \), a little extra thought is involved (but not much more). Sketching the angle and its terminal side, it's easy to notice that we can find a coterminal angle to \( t = 820^ < \circ >\) that is between \( 0^ < \circ >\) and \( 360^ < \circ >\). Subtracting \( 720^ < \circ >\), we arrive at the coterminal angle \( 100^ < \circ >\) (see the figures below). We are now back to the simpler case of a quadrant II angle. To find the reference angle, we imagine we rotated to the negative \( x \)-axis (\( 180^ < \circ >\)) and then backed off by \( \hat \) to arrive at \( 100^ < \circ >\). Mathematically, this means\[ 180^ < \circ >- \hat = 100^ < \circ >\implies \hat = 80^< \circ >. \nonumber \]

While you should strive for understanding in mathematics over memorization, some students initially find the following guidelines helpful until they get used to reference angles. Trust me when I say you want to use the following guideline only for a while - it's too bulky.

Let \( \theta \) be an angle in standard position.

1. If \( 0^ < \circ >\lt \theta \lt 360^ < \circ >\), let \( t = \theta \).
2. If \( \theta \) is not between \( 0^ < \circ >\) and \( 360^ < \circ >\), then let \( t \) be the angle coterminal to \( \theta \) that is between \( 0^ < \circ >\) and \( 360^ < \circ >\).

Caution: Reference Angles are Acute

By definition, reference angles are acute angles. This means they are not \( 0^ < \circ >\) or \( 90^ < \circ >\). In fact, quadrantal angles do not have reference angles.

Checkpoint \(\PageIndex\)

Draw the angle and state its reference angle.

Evaluating Trigonometric Functions Using Reference Angles

We can use reference angles to help us evaluate a trigonometric function at a non-acute angle \( \theta \). To do so, we construct a reference triangle for \( \theta \) using the following method:

1. Choose a point \(P\) on the terminal side of \( \theta \).
2. Draw a line from point \(P\) perpendicular to the \(x\)-axis.

The figure below shows angles \(\theta\) in all four quadrants and the reference angle, \(\hat\), for each. Study the figures, and make sure you understand how to find the reference angle in each quadrant.

Figures \( \PageIndex < 1a >\) (left) and \( \PageIndex < 1b >\) (right): Reference triangles for Quadrant I and Quadrant II angles, respectively.

Figures \( \PageIndex < 1c >\) (left) and \( \PageIndex < 1d >\) (right): Reference triangles for Quadrant III and Quadrant IV angles, respectively.

Summary

These observations may help you remember the formulas:

• The right triangle formed in this way always lies between the terminal side and the \(x\)-axis.
• The positive acute angle formed between the terminal side and the \(x\)-axis is the reference angle, and the right triangle is the reference triangle.

The following activity reveals the usefulness of reference angles and reference triangles when evaluating trigonometric functions of non-acute angles.

Activity: Reference Angles

1. Use a protractor to draw an angle of \(56^\) in standard position. Draw its reference triangle.
2. Use your calculator to find the sine and cosine of \(56^\), rounded to two decimal places. Label the sides of the reference triangle with their lengths.
3. What are the coordinates of the point \(P\) where your angle intersects the unit circle?
4. Draw the reflection of your reference triangle across the \(y\)-axis so that you have a congruent triangle in the second quadrant.
5. You now have the reference triangle for a second-quadrant angle in standard position. What is that angle?
6. Use your calculator to find the sine and cosine of your new angle. Label the coordinates of the point \(Q\) where the angle intersects the unit circle.
7. Draw the reflection of your triangle from part (d) across the \(x\)-axis so that you have a congruent triangle in the third quadrant.
8. You now have the reference triangle for a third-quadrant angle in standard position. What is that angle?
9. Use your calculator to find the sine and cosine of your new angle. Label the coordinates of the point \(R\) where the angle intersects the unit circle.
10. Draw the reflection of your triangle from part (g) across the \(y\)-axis so that you have a congruent triangle in the fourth quadrant.
11. You now have the reference triangle for a fourth-quadrant angle in standard position. What is that angle?
12. Use your calculator to find the sine and cosine of your new angle. Label the coordinates of the point where the angle intersects the unit circle.
13. Generalize: All four of your angles have the same reference angle, \(56^\). For each quadrant, write a formula for the angle whose reference angle is \(\theta\).
    1. Quadrant I:
    2. Quadrant II:
    3. Quadrant III:
    4. Quadrant IV:

    In all four versions of Figure \( \PageIndex < 1 >\), coordinate trigonometry states that\[ \begin
    \sin\left( \theta \right) & = & \dfrac & \quad & \csc\left( \theta \right) & = & \dfrac \\
    \cos\left( \theta \right) & = & \dfrac & \quad & \sec\left( \theta \right) & = & \dfrac \\
    \tan\left( \theta \right) & = & \dfrac & \quad & \cot\left( \theta \right) & = & \dfrac \\
    \end \nonumber \]However, it is also true that in all four versions of Figure \( 1 \), the side of the reference triangle opposite \( \hat \) has length \( |y| \), the side of the reference triangle adjacent to \( \hat \) has length \( |x| \), and the hypotenuse of the reference triangle has a length of \( r \). Therefore, by right triangle trigonometry,\[ \begin
    \sin\left( \hat \right) & = & \dfrac<|y|> & \quad & \csc\left( \hat \right) & = & \dfrac <|y|>\\
    \cos\left( \hat \right) & = & \dfrac<|x|> & \quad & \sec\left( \hat \right) & = & \dfrac <|x|>\\
    \tan\left( \hat \right) & = & \dfrac<|y|> <|x|>& \quad & \cot\left( \hat \right) & = & \dfrac<|x|> <|y|>\\
    \end \nonumber \]Thus, the values of the trigonometric functions of the angle \( \theta \) match the values of the trigonometric functions of \( \hat \), except, possibly, for a difference in sign. The sign of the trigonometric function's value can be determined by the quadrant in which the terminal side of the angle lies. This result is summarized in the following theorem.

    Theorem: Reference Angle Theorem

    The value of a trigonometric function of any angle is equal to that of the function at its reference angle, except for sign. The quadrant determines the sign of the function.

    In the previous chapter, we used a calculator to approximate the values of the trigonometric functions at acute angles. Your calculator can easily find the value of a trigonometric function at any angle. We showcase this in the following example.

    Example \( \PageIndex < 2 >\)

    

    1. Find the reference angle for \(200^\).
    2. Sketch \(200^\) and its reference angle in standard position, along with the reference triangle. Verify that both angles have the same trigonometric values, up to sign.
    Solutions
    1. In standard position, an angle of \(200^\) lies in the third quadrant. Therefore, we rotate to \( 180^ < \circ >\) and add the reference to get to \( 200^ < \circ >\). Therefore, the reference angle is\[200^ - 180^ = 20^ = \hat\nonumber \]
    2. Both angles are shown in the figure below. You can use your calculator to verify the following values.\[ \begin
       \sin \left(20^\right) & \approx & 0.3420 & \quad & \sin \left(200^\right) & \approx & -0.3420 \\
       \cos \left(20^\right) & \approx & 0.9397 & \quad & \cos \left(200^\right) & \approx & -0.9397 \\
       \tan \left(20^\right) & \approx & 0.3640 & \quad & \tan \left(200^\right) & \approx & 0.3640 \\
       \end \nonumber \]

    Note that the results in Example \( \PageIndex < 2 >\) align with what we said previously - the sign of the trigonometric function's value can be determined by the quadrant in which the terminal side of the angle lies. Thus, to compute \( \sin\left( 200^ < \circ >\right) \), we could note that \( \theta \in \mathrm \) and the reference angle is \( 20^ < \circ >\). Since the sine is negative in \( \mathrm \), we get\[ \begin
    \sin\left( 200^ < \circ >\right) & = & \fbox \sin\left( 20^ < \circ >\right) & \quad & \left( \sin\left( \theta \right) \text< is equal to >\sin\left( \hat \right), \text < except for, possibly, the sign>\right) \\
    & = & - \sin\left( 20^ < \circ >\right) & \quad & \left( \text200^ < \circ >\in \mathrm, \text < sine is negative>\right) \\
    \end \nonumber \]From this point forward in Trigonometry, the following Trigonometry Mantra will be helpful.

    Trigonometry is about two things - reference angles and quadrants.

    While this mantra oversimplifies the subject, most of Trigonometry is easier once you know the reference angle and quadrant for a given angle.

    Checkpoint \( \PageIndex < 2 >\)

    1. Find the reference angle for \(285^\).
    2. Sketch \(285^\) and its reference angle in standard position, along with the reference triangle. Verify that both angles have the same trigonometric ratios, up to sign.
    1. \(75^\)
    2. \(\sin \left(285^\right) = -\sin \left(75^\right) \approx -0.9659, \cos \left(285^\right) = \cos \left(75^\right) \approx 0.2588, \tan \left(285^\right) = -\tan \left(75^\right) \approx -3.7321\)

    When combined with the Reference Angle Theorem, the following corollary improves the speed with which we can evaluate trigonometric functions.

    Corollary

    For any integer \( n \),\[ \begin
    \sin\left( \theta + 360^< \circ >n \right) & = & \sin\left( \theta \right) & \quad & \csc\left( \theta + 360^< \circ >n \right) & = & \csc\left( \theta \right) \\
    \cos\left( \theta + 360^< \circ >n \right) & = & \cos\left( \theta \right) & \quad & \sec\left( \theta + 360^< \circ >n \right) & = & \sec\left( \theta \right) \\
    \tan\left( \theta + 360^< \circ >n \right) & = & \tan\left( \theta \right) & \quad & \cot\left( \theta + 360^< \circ >n \right) & = & \cot\left( \theta \right) \\
    \end \nonumber \]

    This result is from our previous discussion that the value of a trigonometric function is the same for all angles coterminal with the original given angle.

    An Additional Note About the Tangent

    As we will investigate later, it turns out that\[ \tan\left( \theta + 180^< \circ >n \right) = \tan\left( \theta \right) \quad \text \quad \cot\left( \theta + 180^< \circ >n \right) = \cot\left( \theta \right) \nonumber \]for any integer \( n \); however, this is not needed for our current discussion.

    Let's see how this corollary, along with focusing on reference angles and quadrants, speeds up the evaluation of trigonometric functions whose reference angles are the special angles.

    Example \(\PageIndex\)

    Find the exact value of each trigonometric function.

    1. \( \cos\left( 225^ < \circ >\right) \)
    2. \( \cot\left( 120^ < \circ >\right) \)
    3. \( \tan\left( -210^ < \circ >\right) \)
    4. \( \sin\left( 690^ < \circ >\right) \)
    1. We quickly note that \( 225^ < \circ >\in \mathrm \) and the reference angle is \( \hat = 45^ < \circ >\). Thus, \[ \begin
       \cos\left( 225^ < \circ >\right) & = & \fbox \cos\left( 45^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & -\cos\left( 45^ < \circ >\right) & \quad & \left( \text\mathrm \right) \\
       & = & -\dfrac> & \quad & \\
       \end \nonumber \]
    2. \( 120^ < \circ >\in \mathrm \) and the reference angle is \( \hat = 60^ < \circ >\). Thus, \[ \begin
       \cot\left( 120^ < \circ >\right) & = & \fbox \cot\left( 60^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & -\cot\left( 60^ < \circ >\right) & \quad & \left( \text\mathrm \right) \\
       & = & -\dfrac> & \quad & \\
       \end \nonumber \]
    3. While we could solve this problem by rotating clockwise by \( 210^ < \circ >\), let's use the corollary.\[ \begin
       \tan\left( -210^ < \circ >\right) & = & \tan\left( -210^ < \circ >+ 360^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & \tan\left( 150^ < \circ >\right) & \quad & \\
       & = & \fbox \tan\left( 30^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & -\tan\left( 30^ < \circ >\right) & \quad & \left( 150^ < \circ >\in \mathrm \text< and tangent is negative in >\mathrm \right) \\
       & = & -\dfrac> & \quad & \\
       \end \nonumber \]
    4. \[ \begin
       \sin\left( 690^ < \circ >\right) & = & \sin\left( 690^ < \circ >- 360^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & \sin\left( 330^ < \circ >\right) & \quad & \\
       & = & \fbox \sin\left( 30^ < \circ >\right) & \quad & \left( \text \right) \\
       & = & -\sin\left( 30^ < \circ >\right) & \quad & \left( 330^ < \circ >\in \mathrm \text< and sine is negative in >\mathrm \right) \\
       & = & -\dfrac& \quad & \\
       \end \nonumber \]

    Checkpoint \(\PageIndex\)

    Find the exact value of each trigonometric function (without touching a calculator).

    1. \( \sin\left( 210^ < \circ >\right) \)
    2. \( \sec\left( -780^ < \circ >\right) \)
    3. \( \sin\left( 405^ < \circ >\right) \)
    1. \( -\frac\)
    2. \( 2 \)
    3. \( \frac<\sqrt> \)

    Finding Non-Acute Angles

    We now turn our attention back to finding angles given values of trigonometric functions. Last chapter, we were able to find \( \theta \) such that \( \tan\left( \theta \right) = 0.5662 \). At that time, we used the \( \mathrm^ \) button on our calculator to find \( \tan^\left( 0.5662 \right) \approx 29.5185^ < \circ >\). At that time, however, we were only working with right triangle trigonometry, and the angles we were interested in were all acute. When working with non-acute angles, the inverse trigonometric functions can get tricky.

    To avoid the trickiness associated with inverse trigonometric functions (and to give us more time with Trigonometry before diving into the more profound theory of the inverse trigonometric functions), it's best to think of them as returning reference angles. Since reference angles are always acute, this interpretation works with what we did in the last chapter; however, as we have seen in this section, we are now dealing with angles that are not necessarily acute.

    For now, think of the inverse trigonometric functions as returning reference angles.

    We must evaluate the inverse trigonometric function at a positive value to return a reference angle. The reason for this cannot be fully justified at this time. Still, we can say that, for example, \( \sin^< -1 >\left( -0.31 \right) \) returns an angle \( \theta \) so that \( \sin\left( \theta \right) = -0.31\); however, we know that the values of all trigonometric functions are positive in \( \mathrm \). Since we want the returned angle to be a reference angle, it must be acute (and, therefore, in the first quadrant). Hence, there is no possibility for a reference angle to be returned if the argument of our inverse trigonometric function is negative.

    If we agree that inverse trigonometric functions evaluated at positive numbers return reference angles, we can ask for solutions to equations involving trigonometric functions.

    For example, find \( \theta \) if \[ \sin\left( \theta \right) = -0.31, \nonumber \]where \( \theta \in \mathrm \).

    First, it should make sense that \( \theta \) could be in the third quadrant because the sine at \( \theta \) is negative, and the sine is negative in the third quadrant (as well as in the fourth quadrant). Remember, Trigonometry is about two things - reference angles and quadrants. We have already been given a quadrant. We evaluate the inverse sine function at \( |-0.31| = 0.31 \) to find the reference angle. Hence, the reference angle is\[ \hat = \sin^\left( |-0.31| \right) = \sin^\left( 0.31 \right) \approx 18.1^< \circ >. \nonumber \]The angle in \( \mathrm \) with reference angle \( \hat \approx 18.1^ < \circ >\) is \( \theta = 180^ < \circ >+ \hat \approx 180^ < \circ >+ 18.1^ < \circ >= 198.1^< \circ >. \)

    Summary

    To find the angle \( \theta \) so that the trigonometric function of \( \theta \) is a given ratio:

    1. Reference Angle. Use the inverse trigonometric function of the absolute value of the given ratio to determine the reference angle, \( \hat \).
    2. Quadrant. Use the given information within the problem to "lock down" the quadrant in which \( \theta \) terminates.
    3. Actual Angle. Use the reference angle and quadrant from (1) and (2) to determine \( \theta \).

    The second step in the summary above assumes you are given extra information to help determine the quadrant in which \( \theta \) terminates. While this will be true in this section, we will eventually shed that requirement. We will begin to find all angles that make a given trigonometric equation valid.

    Example \(\PageIndex\)

    Find \( \theta \) to the nearest tenth of a degree, if \( 0^ < \circ >\lt \theta \lt 360^ < \circ >\).

    1. \( \cos\left( \theta \right) = -0.8457 \), where \( \theta \in \mathrm \).
    2. \( \tan\left( \theta \right) = -1.9122 \), where \( \sin\left( \theta \right) \lt 0 \).
    3. \( \csc\left( \theta \right) = 2.1174\), where \( \cos\left( \theta \right) \lt 0 \).
    1. Reference Angle. We start by finding the reference angle using the absolute value of the given ratio.\[ \hat = \cos^\left( |-0.8457| \right) = \cos^\left( 0.8457 \right) \approx 32.3^ < \circ >\nonumber \]
       Quadrant. Luckily, we were explicitly given the quadrant in which \( \theta \) terminates as \( \mathrm \).
       Actual Angle. Thus,\[ \theta = 180^ < \circ >+ \hat \approx 180^ < \circ >+ 32.3^ < \circ >= 212.3^< \circ >. \nonumber \]
    2. Reference Angle.\[ \hat = \tan^\left( |-1.9122| \right) = \tan^\left( 1.9122 \right) \approx 62.4^ < \circ >\nonumber \]Quadrant. This example requires a little extra thought than part (a). We are given that both the angle's sine and tangent are negative. The sine is negative in quadrants III and IV, while the tangent is negative in quadrants II and IV. The quadrant where both of these conditions are true is quadrant IV.
       Actual Angle. Hence,\[ \theta = 360^ < \circ >- \hat \approx 360^ < \circ >- 62.4^ < \circ >= 297.6^< \circ >. \nonumber \]
    3. Reference Angle. Since our calculator (or other technology) does not have an inverse cosecant button, we begin by rewriting the given equation using the Ratio Identities.\[ \csc\left( \theta \right) = 2.1174 \implies \dfrac<\sin\left( \theta \right)>= 2.1174 \implies \dfrac= \sin\left( \theta \right) \nonumber \]Therefore,\[ \hat = \sin^\left( \dfrac\right) \approx 28.2^< \circ >. \nonumber \]Quadrant. The cosecant is positive in the same quadrants the sine is positive - namely, \( \mathrm \) and \( \mathrm \). The cosine is negative in \( \mathrm \) and \( \mathrm \). Therefore, the quadrant where \( \theta \) terminates will be the shared quadrant, which is \( \mathrm \).
       Actual Angle. Thus,\[ \theta = 180^ < \circ >- \hat \approx 180^ < \circ >- 28.2^ < \circ >= 151.8^< \circ >. \nonumber \]

    Checkpoint \( \PageIndex < 4 >\)

    1. Solve \( \sec\left( \theta \right) = -1.8 \), where \( 90^ < \circ >\lt \theta \lt 180^ < \circ >\). Round your answer to the nearest tenth of a degree.
    2. Find the sine of \( \theta \) given that \(\tan \left(\theta\right)=-2\), \( \cos\left( \theta \right) \gt 0 \), and \( 0^ < \circ >\lt \theta \lt 360^ < \circ >\). Round your answer to four decimal places.
    1. \(\theta \approx 123.7^< \circ >\)
    2. \(\sin\left(\theta\right) \approx -0.8944\)

    Of course, if given a "special" trigonometric ratio, you should not reach for a calculator.

    Example \(\PageIndex\)

    Find \( \alpha \) if \( \cos\left( \alpha \right) = -\frac> \) and \( \alpha \in \mathrm \), where \( 0^ < \circ >\lt \alpha \lt 360^ < \circ >\).

    Solution Reference Angle. It is crucial that you recognize the special ratios. Sketching the \( 30^ < \circ >\)-\( 60^ < \circ >\)-\( 90^ < \circ >\) triangle, we see that the reference angle for which \( \cos\left( \alpha \right) = \left|-\frac>\right| = \frac> \) is \( \hat = 30^ < \circ >\).
    Quadrant. \( \alpha \in \mathrm \)
    Actual Angle. Thus,\[ \alpha = 180^ < \circ >- \hat = 180^ < \circ >- 30^ < \circ >= 150^< \circ >. \nonumber \]

    Checkpoint \(\PageIndex\)

    Solve \( \tan\left( \beta \right) = -\sqrt \) given \( 0^ < \circ >\lt \beta \lt 360^ < \circ >\) and \( \cos\left( \beta \right) \gt 0 \).

    Answer

    Homework

    Vocabulary Check

    1. The ___ for \(\theta\) is the positive acute angle formed between the terminal side of \(\theta\) and the \(x\)-axis.

    Concept Check

    1. Camille wants an obtuse angle, \(\theta\), that satisfies \(\sin \left(\theta\right)=0.3\). Ivan presses some buttons on his calculator and reports that \(\theta \approx 17.46^\). Explain Ivan's error and give a correct approximation of \(\theta\) accurate to two decimal places.

    True or False? For Problems 3 - 4, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

    1. To construct a reference triangle for an angle, we must choose a point \(P\) on the terminal side of \( \theta \) and draw a line from point \(P\) perpendicular to the \(y\)-axis.
    2. The trigonometric ratios of any angle are equal to the ratios of its reference angle, except for sign. The sign of the ratio is determined by the quadrant.

    Basic Skills

    1. Give the lengths of the legs and the hypotenuse of each right triangle.
       1. 
       2. 
    2. Explain why the length of the horizontal leg of the right triangle is \(−x\).

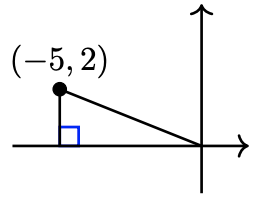
    For Problems 7 - 14, find the reference angle for the given angle. Make a sketch showing the angle, the reference angle, and the reference triangle.

    1. \(\theta = 100^\)
    2. \(A = 125^\)
    3. \(\beta = 216^\)
    4. \( \theta = 194^ < \circ >\, 15^ <\prime>\)
    5. \(\alpha = 242^\)
    6. \(\phi = 297^\)
    7. \( \lambda = 137^ < \circ >\, 50^ <\prime>\)
    8. \(\theta = 336^\)

    For Problems 15 - 20, find three angles between \(90^\) and \(360^\) having the given reference angle, and sketch all four angles on the same grid.

    For Problems 21 - 35, find the exact value of the trigonometric function using reference angles and quadrants (do not use a calculator).

    1. \( \cos\left( 120^ < \circ >\right) \)
    2. \( \sin\left( 135^ < \circ >\right) \)
    3. \( \tan\left( 150^ < \circ >\right) \)
    4. \( \sec\left( 225^ < \circ >\right) \)
    5. \( \sin\left( 240^ < \circ >\right) \)
    6. \( \cot\left( 210^ < \circ >\right) \)
    7. \( \csc\left( 330^ < \circ >\right) \)
    8. \( \cos\left( 315^ < \circ >\right) \)
    9. \( \sin\left( 300^ < \circ >\right) \)
    10. \( \cos\left( -150^ < \circ >\right) \)
    11. \( \sin\left( -210^ < \circ >\right) \)
    12. \( \sec\left( -315^ < \circ >\right) \)
    13. \( \sin\left( 585^ < \circ >\right) \)
    14. \( \cos\left( 840^ < \circ >\right) \)
    15. \( \tan\left( -585^ < \circ >\right) \)

    For Problems 36 - 43, use the values below to find the value of the trigonometric function. Do not use a calculator!
    \(\cos \left(23^\right) \approx 0.9205 \quad \sin \left(46^\right) \approx 0.7193 \quad \tan \left(78^\right) \approx 4.7046\)

    

    1. \(\cos \left(157^\right)\)
    2. \(\sin \left(226^\right)\)
    3. \(\csc \left(314^\right)\)
    4. \(\sec \left(203^\right)\)
    5. \(\tan \left(258^\right)\)
    6. \(\cot \left(282^\right)\)
    7. \(\sin \left(-134^\right)\)
    8. \(\cos \left(-383^\right)\)
    9. On the circle in the figure, all angles are shown in standard position. Find the measure in degrees of the angles labeled (a) - (i) and state their reference angles.
    10. 1. Draw three angles, one in each quadrant except the first, whose reference angle is \(60^\).
        2. Find exact values for the sine, cosine, and tangent of each angle in part (a).
    11. 1. Draw three angles, one in each quadrant except the first, whose reference angle is \(30^\).
        2. Find exact values for the sine, cosine, and tangent of each angle in part (a).
    12. 1. Draw three angles, one in each quadrant except the first, whose reference angle is \(45^\).
        2. Find exact values for the sine, cosine, and tangent of each angle in part (a).
    13. Complete the table with exact values.

        \(\theta\)

        \(30^\)

        \(45^\)

        \(60^\)

        \(120^\)

        \(135^\)

        \(150^\)

        \(210^\)

        \(225^\)

        \(240^\)

        \(300^\)

        \(315^\)

        \(330^\)

        \(\sin \left(\theta\right)\)

        \(\cos \left(\theta\right)\)

        \(\tan \left(\theta\right)\)

        \(\csc \left(\theta\right)\)

        \(\sec \left(\theta\right)\)

        \(\cot \left(\theta\right)\)

        For Problems 49 - 54, find a second angle between \(0^\) and \(360^\) with the given trigonometric ratio.

        1. \(\sin \left(75^\right)\)
        2. \(\cos \left(32^\right)\)
        3. \(\tan \left(84^\right)\)
        4. \(\csc \left(16^\right)\)
        5. \(\sec \left(47^\right)\)
        6. \(\cot \left(56^\right)\)

        For Problems 55 - 69, use the given information to find an approximation of \( \theta \) to the nearest degree if \(0^ \le \theta \lt 360^\).

        1. \(\tan \left(\theta\right) = 8.1443\) with \( \theta \in \mathrm \)
        2. \(\sin \left(\theta\right)=0.7880\) with \( \theta \in \mathrm \)
        3. \(\cos \left(\theta\right)=0.9205\) with \( \theta \in \mathrm \)
        4. \(\tan \left(\theta\right)=-3.4874\) with \( \theta \in \mathrm \)
        5. \(\sin \left(\theta\right)=-0.9962\) with \( \theta \in \mathrm \)
        6. \(\cos \left(\theta\right)=-0.0349\) with \( \theta \in \mathrm \)
        7. \(\sin \left(\theta\right)=0.8381\) where \( \cos\left(\theta\right) \gt 0 \)
        8. \(\tan \left(\theta\right)=-2.1728\) where \( \sin\left(\theta\right) \gt 0 \)
        9. \(\cos \left(\theta\right)=-0.2155\) where \( \tan\left(\theta\right) \gt 0 \)
        10. \(\sin \left(\theta\right)=-0.1179\) where \( \tan\left(\theta\right) \lt 0 \)
        11. \(\cos \left(\theta\right)=0.1818\) where \( \csc\left(\theta\right) \lt 0 \)
        12. \(\tan \left(\theta\right)=1.7531\) where \( \sec\left(\theta\right) \lt 0 \)
        13. \(\csc \left(\theta\right)=2.8549\) where \( \cos\left(\theta\right) \lt 0 \)
        14. \(\sec \left(\theta\right)=-1.3888\) where \( \csc\left(\theta\right) \gt 0 \)
        15. \(\cot \left(\theta\right)=-0.9411\) where \( \cos\left(\theta\right) \lt 0 \)

        For Problems 70 - 84, use the given information to find the exact value of \( \theta \) if \(0^ \le \theta \lt 360^\). Do not use a calculator!

        1. \(\tan \left(\theta\right) = \sqrt\) with \( \theta \in \mathrm \)
        2. \(\sin \left(\theta\right) = \frac\) with \( \theta \in \mathrm \)
        3. \(\cos \left(\theta\right) = \frac<\sqrt> \) with \( \theta \in \mathrm \)
        4. \(\tan \left(\theta\right) = -1\) with \( \theta \in \mathrm \)
        5. \(\sin \left(\theta\right) = -\frac<\sqrt>\) with \( \theta \in \mathrm \)
        6. \(\cos \left(\theta\right) = -\frac\) with \( \theta \in \mathrm \)
        7. \(\sin \left(\theta\right) = \frac<\sqrt> \) where \( \cos\left(\theta\right) \gt 0 \)
        8. \(\tan \left(\theta\right) = -\frac<\sqrt>\) where \( \sin\left(\theta\right) \gt 0 \)
        9. \(\cos \left(\theta\right) = -\frac<\sqrt>\) where \( \tan\left(\theta\right) \gt 0 \)
        10. \(\sin \left(\theta\right) = -\frac\) where \( \tan\left(\theta\right) \lt 0 \)
        11. \(\cos \left(\theta\right) = \frac\) where \( \csc\left(\theta\right) \lt 0 \)
        12. \(\tan \left(\theta\right) = 1\) where \( \sec\left(\theta\right) \lt 0 \)
        13. \(\csc \left(\theta\right) = 2\) where \( \cos\left(\theta\right) \lt 0 \)
        14. \(\sec \left(\theta\right)= -\frac<\sqrt>\) where \( \csc\left(\theta\right) \gt 0 \)
        15. \(\cot \left(\theta\right)= -\sqrt\) where \( \cos\left(\theta\right) \lt 0 \)

        Synthesis Questions

        For Problems 85 - 90, find exact values for all solutions between \(0^\) and \(360^\).

        1. \(\cos \left(\theta\right)=-\cos \left(24^\right)\)
        2. \(\tan \left(\theta\right)=-\tan \left(9^\right)\)
        3. \(\sin \left(\theta\right)=-\sin \left(66^\right)\)
        4. \(\cos \left(\theta\right)=-\cos \left(78^\right)\)
        5. \(\tan \left(\theta\right)=-\tan \left(31^\right)\)
        6. \(\sin \left(\theta\right)=-\sin \left(42^\right)\)
        7. Later we will be able to show that \(\sin \left(18^\right)=\frac-1>\). What is the exact value of \(\sin \left(162^\right)\)?
        8. Later we will be able to show that \(\cos \left(36^\right)=\frac+1>\). What is the exact value of \(\cos \left(144^\right)\)?

        For Problems 93 - 102,
        (a) Sketch an angle in standard position with the given properties.
        (b) Find \(\cos \left(\theta\right)\), \(\sin \left(\theta\right)\), and \(\tan \left(\theta\right)\).
        (c) Find the angle \(\theta\), rounded to tenths of a degree.

        1. The point (−5, 12) is on the terminal side.
        2. The point (12, 9) is on the terminal side.
        3. \(\cos \left(\theta\right) = −0.8\)
        4. \(\cos \left(\theta\right) = \frac\)
        5. \(\cos \left(\theta\right) = \frac\)
        6. \(\cos \left(\theta\right) = -\frac\)
        7. \(\tan \left(\theta\right) = -\frac\)
        8. \(\tan \left(\theta\right) = \frac\)
        9. \(\tan \left(\theta\right) = 4\)
        10. \(\tan \left(\theta\right) = -1\)

        For Problems 103 - 106,
        (a) Find the sine and cosine of the angle.
        (b) Sketch the supplement of the angle in standard position. (Use congruent triangles.)
        (c) Find the sine and cosine of the supplement.
        (d) Find the angle and its supplement, rounded to the nearest degree.

        1. 
        2. 
        3. 
        4. 

        Problems 107 and 108 refer to the following table of values.

        \(\theta\)	\(15^\)	\(25^\)	\(65^\)	\(75^\)	\(105^\)	\(115^\)	\(155^\)	\(165^\)
        \(\cos \left(\theta\right)\)
        \(\sin \left(\theta\right)\)
        \(\tan \left(\theta\right)\)

        1. Use your calculator to fill in the table. Round values to four decimal places.
        2. For each angle \(\theta\) in the table, the angle \(180^ − \theta\) is also in the table.
           1. What is true about \(\sin \theta\) and \(\sin(180^ − \theta)\)?
           2. What is true about \(\cos \theta\) and \(\cos(180^ − \theta)\)?
           3. What is true about \(\tan \theta\) and \(\tan(180^ − \theta)\)?

           Problems 109 - 114 preview the concept of solving trigonometric equations (a topic reserved for later in the course). For each equation, find two different angles between \( 0^ < \circ >\) and \( 360^ < \circ >\) that satisfy the equation. Round your answers to the nearest \(0.1^\).

           For Problems 115 - 118, fill in the blanks with complements or supplements.

           1. If \(\sin \left(57^\right)=q\), then \(\sin \left(\rule\right) =q\), and \(\cos \left(\rule\right)\) and \(\cos \left(\rule\right)\) both equal \( q \).
           2. If \(\sin \left(18^\right) = w\), then \(\sin \left(\rule\right) = w\), \(\cos \left(\rule\right) = w\), and \(\cos \left(\rule\right) = -w\).
           3. If \(\cos \left(74^\right)=m\), then \(\cos \left(\rule\right) =-m\), and \(\sin \left(\rule\right) \) and \(\sin \left(\rule\right) \) both equal \(m\).
           4. If \(\cos \left(36^\right) = t\), then \(\cos \left(\rule\right) = -t\), and \(\sin \left(\rule\right) \) and \(\sin \left(\rule\right) \) both equal \(t\).
           5. 1. Sketch the line \(y = \dfracx\).
              2. A point on the line with a positive \(x\)-coordinate.
              3. The line \(y = \fracx\) makes an angle with the positive \(x\)-axis. What is that angle?
              4. Repeat parts (a) through (c) for the line \(y = \fracx\), except find a point with a negative \(x\)-coordinate.
              1. Sketch the line \(y = \fracx\).
              2. Find a point on the line with a positive \(x\)-coordinate.
              3. The line \(y = \fracx\) makes an angle with the positive \(x\)-axis. What is that angle?
              4. Repeat parts (a) through (c) for the line \(y = \fracx\), except find a point with a negative \(x\)-coordinate.

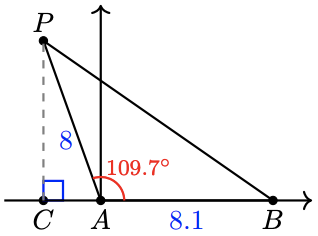
              For Problems 121 and 122,
              (a) Find the coordinates of point \(P\). Round to two decimal places.
              (b) Find the sides \(B C\) and \(P C\) of \(\triangle P C B\).
              (c) Find side \(P B\).

              1. 
              2. 

              Challenge Problems

              1. Why are the sines of supplementary angles equal, but the cosines are not? What about the tangents of supplementary angles?

              This page titled 4.1: Reference Angles is shared under a CC BY-NC 12 license and was authored, remixed, and/or curated by Roy Simpson.

              1. Back to top
              2. • Chapter 4: Radian Measure and the Circular Functions
                 • 4.2: Radian Measure and Arc Length
              • Was this article helpful?
              • Yes
              • No